A NEW AND USEFUL REVIEW
THE FUNDAMENTAL MEASUREMENT OF STONE PROPENSITY
The three Moirai, or the triumph of death, Flemish tapestry ca 1520, Victoria and Albert Museum, London, depicts Clotho, who spins the thread of life, Lachesis, who measures out the length of the thread, and Atropos, the inexorable, who cuts the thread. In book 11 of the Odyssey, Odysseus travels to the underworld where, among other matters, he learns from Tiresias his own ‘fate’; that he will return to his home and his own wife; that he will travel again to a place so far from the sea his oar will go unrecognized; and that he will die in peace, by the sea and among his own people. But he must make an offering in that foreign place to appease Poseidon, who hates him for blinding Polyphemus, and that he must avoid the herds of Helios on Thrinacia, on his way home. His ‘fate’ was fixed, but the path to its inevitable conclusions depended upon his choices.
 I put this picture here, and my brief and shallow comments on the Odyssey, to introduce the overarching power of saturation, which ultimately determines the outcome of a solution. Howsoever important the matrix molecules, they can influence only the kinetics of crystallization. By doing so they can affect which crystals might predominate, and certainly can delay crystallization long beyond the time a crystal resides in the kidneys or urinary tract. But saturation is what powers crystallization; without it nothing. With it, crystals may or may not form in the time you observe it. But a saturated solution is inevitably unstable; it contains a free energy that will eventually manifest itself in loss of precisely that mass which is above the solubility. Saturation is the fate of the solution; all of the kinetic modifiers determine only the path by along which that fate – conversion of free energy into solid phase – progresses.
I put this picture here, and my brief and shallow comments on the Odyssey, to introduce the overarching power of saturation, which ultimately determines the outcome of a solution. Howsoever important the matrix molecules, they can influence only the kinetics of crystallization. By doing so they can affect which crystals might predominate, and certainly can delay crystallization long beyond the time a crystal resides in the kidneys or urinary tract. But saturation is what powers crystallization; without it nothing. With it, crystals may or may not form in the time you observe it. But a saturated solution is inevitably unstable; it contains a free energy that will eventually manifest itself in loss of precisely that mass which is above the solubility. Saturation is the fate of the solution; all of the kinetic modifiers determine only the path by along which that fate – conversion of free energy into solid phase – progresses.
Chem. Soc. Rev., 2014, 43, 2286
This review from the Royal Society of Chemistry is recent and reviews the fundamental physical basis for crystal formation. The topic is vastly complicated when different solvents and solutes are taken together. But what happens in the kidneys can be stated with reasonable simplicity; it is similar to crystallization from variation of concentrations by evaporation (Sections 3 and 4 of this review). The most simple and probably most useful measure presented is simply the ratio of the concentration of the material of interest divided by the concentration at saturation, the so called supersaturation ratio.
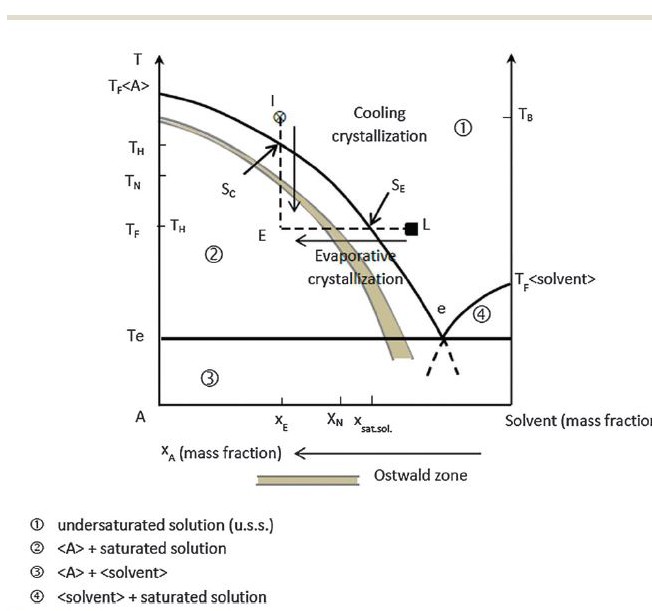
Crystallization process
The diagram shows both processes expressed in mass fractions, the fraction of mass from solute and the fraction from the solvent. We begin with a system with a mass fraction (mass of solute/mass of solute + mass of solvent) of XE which occurs at the temperature TB. This is marked by the circled x on the diagram. The solution is homogeneous – the salt of interest is entirely dissolved and there is no solid phase, only the liquid solvent. The solid curve marks out the relationship between temperature and mass fraction of solute at the point of solubility, the solubility curve. Above that curve, area 1 of the graph, the solution is homogeneous – undersaturated. Along the curve it is saturated.
Crystallization by change of temperature.
Cooling to TH will bring the solution precisely to the solubility line for the mass fraction XE – vertical line from x downward to Sc. There is little likelihood of crystal formation of the solute A in this range. At TN and below spontaneous nucleation of N becomes high and will almost always have occurred by TF given a mass fraction of XE. The Ostwald limit curve is drawn as a band to denote the uncertainty of its exact limits. All points below the limit curve (region 2) are called labile supersaturated, meaning the solution contains the mass A of saturation + <A> the ‘extra’ mass of solid phase and will nucleate spontaneously. Points between Sc and the Ostwald limit are called metastably supersaturated in that the solution holds a concentration of above the solubility curve but not enough to make crystallization likely.
Whereas mass fraction is necessary to discuss solutions with two or more phases – eg solvent and solid phase crystallized A – supersaturation is gauged via concentration of the dissolved A in solution in relation to solubility which up until now we have simply referred to as along the so called solubility curve. What solubility means is that the solution has a concentration of A such that addition of more solid A will result in addition of precisely that mass of A in the solid phase. Of note, the dissolved A and the solid phase of A in such a saturated heterogeneous system are in an equilibrium such that some dissolved A will crystallize and some crystallized A dissolve at a constant mass fraction of solid A. This process selectively involves the smallest crystals so that with time, at a constant mass, the overall crystal size distribution shifts upward – Ostwald ripening.
Given a knowledge of the concentration of A at temperature T in the solution (Csat), supersaturation can be stated as the supersaturation ratio: C/Csat. Relative supersaturation is simply 1 – C/Csat or (C – Csat)/Csat.
Crystallization by evaporation.
At a fixed temperature TF, the point L at a mass ratio below saturation (C<Csat) solvent, water in this case, is removed by evaporation to achieve the concentration Csat, the mass ratio when C = Csat. In the range of supersaturation between X sat sol to XN, the Ostwald limit curve evaporation merely produces a supersaturated solution. Above XN, crystallization begins and SS falls to 1. This process is strongly analogous to what happens in the renal tubules, as water extraction by osmotic concentration will behave as would evaporation with the exception that the rate of water loss is measured in a few minutes so that crystallization cannot occur as slowly as in an evaporating solution. This matter of rates and the final crystal product requires information beyond where we are now, but simply said the solution is unlikely to be in an unsteady state and crystallization will depart from the idealizations of the diagram.
The eutectic point. Though not important for our purposes, it is the temperature at which solid phase A and solid phase – ice – of the solvent coexist with the liquid phase. As the mass fraction of A falls to 0 this temperature rises to the freezing point of pure water. As noted, in the opposite direction, pure A, TF is the melting point of pure A. region 4 is simply the binary region of ice and water for varying concentrations of A. Region 3 is ice; points along the line A are pure A, and those along the right axis are pure water.
TF<A>. This is the temperature at which pure A is liquid – its melting point.
Implications
For any solute in water supersaturation is the gauge that defines the propensity for phase change. At a constant temperature such as in the body, the SS ratio, as an example, defines whether the solution – urine for our purposes here – is undersaturated, metastably supersaturated, or unstably supersaturated provided we have, for the solute of interest, a knowledge of Csat and the Ostwald limits for that temperature. This is a main point of all of stone disease: Supersaturation determines if crystallization can occur, so it is a ruling variable.
From this we can derive what I might call a primary statement for all of stone disease: The urine supersaturation of an active stone former is too high with respect to the crystals of the stones that are being formed. Prevention requires that it be lowered.
SOME RECENT PAPERS
CUAJ 2008;2(2):117-22
The authors point out that SS is the gold standard for assessing crystallization potential, as they are well aware of its role as the driving force for the process of nucleation, growth, and aggregation. Their question was the extent to which conventional urine risk factors expressed as excretions could detect elevated SS values. They used retrospective analysis of data from well studied patients in whom SS had been calculated. They found that elevated levels of calcium or oxalate excretion were sensitive indicators of increased SS values but very non specific. A urine calcium excretion of about 230 in women and 280 mg/day in men were at an optimal point between sensitivity and specificity, but given the poor specificity the approach seemed flawed.
Journal of Endourology. -Not available-, ahead of print. doi:10.1089/end.2014.0077.
Enteric hyperoxaluria is a not uncommon cause of COM stones. Urine calcium is not high and may be low. LIkewise the normal ratio of calcium to oxalate molarity, normally 10 or more is much closer to unity. The authors were moved by these observations to calculate SS, molar ratios and the individual species in urine using not the common EQUIL program but the more elaborate JESS program. Questions included benefits of citrate, of oral calcium to reduce urine oxalate. Of interest, the authors point out the primacy of SS: “Qualitative and quantitative information about the chemical complexes (speciation) in urine is extremely important for evaluating the supersaturation of stone forming salts. This parameter is the gold standard by which the risk of stone formation is assessed..”
Their data were obtained from Vancouver and our own group. These included bowel patients and idiopathic CaOx stone formers and normal people. Models were created by variation of calcium and oxalate values.
Their main findings are that, though low, urine calcium is a critical driver of SS COM being the limiting reagent in the Ca Ox product so that giving calcium and raising urine calcium may not lower SS well.


Hi Fred,
I like the idea of creating this forum but I am not certain how many and what type of comments it will generate. One question I have had about CaOx , crystallization, and stone formation is where do crystals form in an individual with stone growth on RP? Do they form within the nephron and then attach to RP (or proteins coating it), within the calyx and then attach, or do they grow on crystals attached to RP? If they form within a nephron they have the potential to interact with tubular epithelial cells even if such interaction are brief. The could possibly even roll through the nephron with a jerky motion as they briefly attach. This could be sufficient to stimulate a cellular response. This could even precede the formation of RP. Which comes first; crystals or RP?
Hi Ross
In the case of stones formed attached to the RP, crystals may form in the pelvic urine and deposit on the surface of the growing stone or nucleate on the macromolecular coating on stone surface. The calcium phosphate of the plaque may also directly transform into calcium oxalate to start the transition from CaP to CaOx. It is possible, but unlikely for crystals to form in the renal tubules, travel through the nephron and then become a part of the stone.
Hi Fred,
I like the idea of creating this forum but I am not certain how many and what type of comments it will generate. One question I have had about CaOx , crystallization, and stone formation is where do crystals form in an individual with stone growth on RP? Do they form within the nephron and then attach to RP (or proteins coating it), within the calyx and then attach, or do they grow on crystals attached to RP? If they form within a nephron they have the potential to interact with tubular epithelial cells even if such interaction are brief. The could possibly even roll through the nephron with a jerky motion as they briefly attach. This could be sufficient to stimulate a cellular response. This could even precede the formation of RP. Which comes first; crystals or RP?
Hi Ross
In the case of stones formed attached to the RP, crystals may form in the pelvic urine and deposit on the surface of the growing stone or nucleate on the macromolecular coating on stone surface. The calcium phosphate of the plaque may also directly transform into calcium oxalate to start the transition from CaP to CaOx. It is possible, but unlikely for crystals to form in the renal tubules, travel through the nephron and then become a part of the stone.
Two more questions.
First, is it known if there are any differences in the Ostwald limit between people who don’t form calcium stones, and people who will form calcium stones stones in the future but have not formed any so far, or between people with and without a family history of stones?
Second, you have described the inhibitors of stone formation in urine working by reducing Ca++ available for stone formation by complexing with it, or by binding to crystal surfaces and disrupting epitaxial growth. Is there any evidence that that these inhibitors might also alter the solubility of Ca oxalate or phosphate (other than by changing pH)? Given the very high SS of urine with respect to Ca oxalate, one would expect the formation of Ca oxalate crystals to be essentially irreversible regardless of any slight change in solubility. But it could be different for Ca phosphates with their much lower SS.
In realize that it may not be possible to draw a distinction between making Ca++ unavailable for crystal formation and increasing solubility.
If you mean experimentally, one can distinguish for citrate which binds mole on mole with calcium. For most inhibitors molar concentrations for inhibition are micromolar or less so calcium binding is irrelevant and effects must be on crystals themselves. Apparent solubilities can be affected if transformation to a more insoluble crystal form occurs; for example if one blocks conversion of brushite to apatite. Regards, Fred
There is; here is the article. I know of no way inhibitors can act apart from direct interactions with crystals. The mode of their interactions can be complex in that larger anionic molecules can bind at many calcium sites and those with amphiphilic properties can cover calcium sites cooperatively and offer the solution its hydrophobic surface which minimizes secondary nucleation on the inhibitor itself. Regards, Fred
Two more questions.
First, is it known if there are any differences in the Ostwald limit between people who don’t form calcium stones, and people who will form calcium stones stones in the future but have not formed any so far, or between people with and without a family history of stones?
Second, you have described the inhibitors of stone formation in urine working by reducing Ca++ available for stone formation by complexing with it, or by binding to crystal surfaces and disrupting epitaxial growth. Is there any evidence that that these inhibitors might also alter the solubility of Ca oxalate or phosphate (other than by changing pH)? Given the very high SS of urine with respect to Ca oxalate, one would expect the formation of Ca oxalate crystals to be essentially irreversible regardless of any slight change in solubility. But it could be different for Ca phosphates with their much lower SS.
In realize that it may not be possible to draw a distinction between making Ca++ unavailable for crystal formation and increasing solubility.
If you mean experimentally, one can distinguish for citrate which binds mole on mole with calcium. For most inhibitors molar concentrations for inhibition are micromolar or less so calcium binding is irrelevant and effects must be on crystals themselves. Apparent solubilities can be affected if transformation to a more insoluble crystal form occurs; for example if one blocks conversion of brushite to apatite. Regards, Fred
There is; here is the article. I know of no way inhibitors can act apart from direct interactions with crystals. The mode of their interactions can be complex in that larger anionic molecules can bind at many calcium sites and those with amphiphilic properties can cover calcium sites cooperatively and offer the solution its hydrophobic surface which minimizes secondary nucleation on the inhibitor itself. Regards, Fred
When SS is calculated by programs like EQUIL, how is “saturation” (SS=1) defined? Is it the saturation ion concentrations of pure water at a given T and pH, or is it a value calculated separately for each urine sample? Or is it assumed that the the two values (for pure water and for individual urine samples) do not differ enough to make a practical difference?
Hi Joe, the concentration of the stone forming salt – like calcium oxalate – is calculated for the urine using all of the equilibria in which calcium and oxalate participate. The solubility of calcium oxalate salt at 37 degrees is known – the effects of ionic strength pH etc are already in the initial calculation – and the ratio is calculated as the salt concentration divided by the solubility concentration. Fred Coe
When SS is calculated by programs like EQUIL, how is “saturation” (SS=1) defined? Is it the saturation ion concentrations of pure water at a given T and pH, or is it a value calculated separately for each urine sample? Or is it assumed that the the two values (for pure water and for individual urine samples) do not differ enough to make a practical difference?
Hi Joe, the concentration of the stone forming salt – like calcium oxalate – is calculated for the urine using all of the equilibria in which calcium and oxalate participate. The solubility of calcium oxalate salt at 37 degrees is known – the effects of ionic strength pH etc are already in the initial calculation – and the ratio is calculated as the salt concentration divided by the solubility concentration. Fred Coe
I am more concerned with the uric acid stone. I am also very concerned how the potassium in potassium citrate pills lower blood pressure. My blood pressure tends to be low and lack of energy occurs when it gets lowered.
Hi Helen, I gather your stones are composed of uric acid. If so, potassium citrate is an ideal prevention and used properly should prevent more stones. Potassium salts do lower blood pressure but not to pathological levels, so you should be fine with the medication. It requires medical supervision, of course. Regards, Fred Coe
I am more concerned with the uric acid stone. I am also very concerned how the potassium in potassium citrate pills lower blood pressure. My blood pressure tends to be low and lack of energy occurs when it gets lowered.
Hi Helen, I gather your stones are composed of uric acid. If so, potassium citrate is an ideal prevention and used properly should prevent more stones. Potassium salts do lower blood pressure but not to pathological levels, so you should be fine with the medication. It requires medical supervision, of course. Regards, Fred Coe