 The citrate molecule in urine not only binds calcium and therefore reduces supersaturation with respect to the calcium stone forming crystals but hinders the formation and growth of such crystals. Modern techniques permit scientists to visualize these effects of citrate, and other molecules, rather directly, and to quantify them.
The citrate molecule in urine not only binds calcium and therefore reduces supersaturation with respect to the calcium stone forming crystals but hinders the formation and growth of such crystals. Modern techniques permit scientists to visualize these effects of citrate, and other molecules, rather directly, and to quantify them.
The reference I give above is outstanding as an exposition of the citrate and osteopontin effects of calcium oxalate, and therefore I have chosen it as my basis for this article. A wider ranging article is also outstanding, for those of us who love this topic.
HOW CRYSTALS GROW
Plates
Being, as I am, a mere reader of the elaborate and rather abstruse field of crystal kinetics, I can say about crystal growth only the most banal and simple things. But for most of us these suffice. For my purpose here is to show that citrate does slow crystal formation, and how, in general terms, it does so.
The left hand picture on the featured illustration shows the ‘top’ of a calcium oxalate mono hydrate crystal. It has grown a lot like one of the great pyramids with which long dead Pharaohs sought immortality. Innumerable plates of crystal stack one on the other somewhat the way I have stacked pancakes before pouring maple syrup over the lot.
Steps
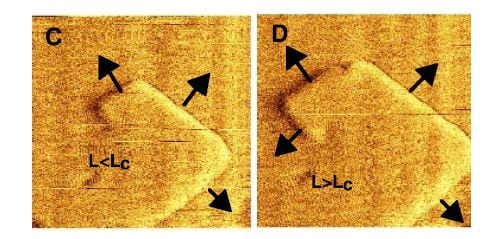 These plates arise as steps that grow up out of flat terraces. The terrace is the flat base in both panels in the figure at left, the step the raised portion. Now here is critical part to understand: Ions – like calcium and oxalate – leave the surfaces at rates determined almost only by temperature, but add in proportion to their concentrations in solution. When the off and on rates are the same, the system of crystals and solution is at equilibrium and this is how solubility is defined: Crystals neither grow nor shrink. Higher concentrations create supersaturations, which cause crystals to grow.
These plates arise as steps that grow up out of flat terraces. The terrace is the flat base in both panels in the figure at left, the step the raised portion. Now here is critical part to understand: Ions – like calcium and oxalate – leave the surfaces at rates determined almost only by temperature, but add in proportion to their concentrations in solution. When the off and on rates are the same, the system of crystals and solution is at equilibrium and this is how solubility is defined: Crystals neither grow nor shrink. Higher concentrations create supersaturations, which cause crystals to grow.
The reason why the off rate depends on temperature is that what holds ions like calcium and oxalate on the crystal surface is their bonds with one another, essentially the bonds that make up the crystal structure. Higher temperature means a higher rate of random movement of molecules, and such movement can break bonds by separating molecules from one another. As new ions add, those that can make the most bonds will be most likely to stay. It is at the edge of a step where bonds are easiest to make, so this is where growth will occur.
At the same time, bonds are easiest to make because the number of bonding sites is lowest – the edge is thin and there are not as many ions as on the flat plane. Because there are less bonds made the off rate will be high. As a result, the edges of steps are the active regions of crystals. Their active growth, shown in direction by the arrows, causes them to spiral as in the right hand plate of the figure.
Where do steps arise? Sometimes, an island of new crystal will form on on a terrace and make a step. Mostly, the crystal has defects, breaks in the lattice, which make steps.
Islands and Free Energy
In case you have not read about crystals lately, here is a region of thought you might want to enter with considerable fear and fortified by faith that nature’s beauty will repay, eventually, the travails of such a pilgrimage.
WHY SHOULD ISLANDS FORM?
Imagine a flat terrace bathed by a solution that contains, in our example, calcium and oxalate. Why will such ions park themselves on that terrace to make an island?
It is all a matter of changes in free energy. But changes with respect to what?
The bulk crystal, in which calcium and oxalate ions are enmeshed in multiple bonds is the reference point. The solution is the other point. When an ion leaves the solution to join the terrace, and become bonded there, free energy falls – it is a thermodynamically favored outcome. That is a short answer as to why islands will form.
But – that word! – the fall in free energy is less than that as measured from the solution to the bulk crystal – where molecules are bonded more fully. This difference is termed the surface energy – the difference between molecules at the surface and within the crystal.
Even worse, when an island begins to form, the base of a step, there is an additional energy at the edge – where bonds are most scarce. We have encountered this step energy just above. On the one hand, there is a tendency to form the step because free energy is below that of the solution. On the other hand, the edge has a higher free energy – off rate – than the bulk crystal because of its paucity of bonds.
The balance is interesting – look closely. The on force is proportional to the number of molecules in the island. That makes sense because more molecules, more bonds. The off force is proportional to the edge surface at risk – the length of the perimeter.
The proportion between the volume and circumference will be proportional to the radius: higher radius, the smaller the ratio of surface to volume. This is true for any shaped object. There will also always be radius – the ‘critical radius’ – at which the two forces match. Above that, growth will be favored as a way of lowering free energy – adding bonds. Below that radius, free energy will fall as the island dissolves.
As a result smaller islands will tend to dissolve and those lucky enough to become large will grow larger. Does this not remind us of income inequality? Is nature not beautiful, and strange in how it instructs us?
I will not walk us through the steps – no pun – but it is true that the exact same reasoning will relate to growth of step edges growing up from the base of an island. Likewise, it is obvious that new islands will almost always tend to form where the terrace is disrupted – offers an edge – because of dislocations.
GIBBS – THOMSON (G-T) RELATIONSHIP
You can imagine – if you have even read the foregoing – that solution supersaturation is crucial. The higher it is, the smaller the island that can survive. The relationship between the critical radius and supersaturation is described by the G-T function. The actual relationship for a crystal can be determined, and from the measurements one can calculate the step edge energy – which is where we started.
G – T AND CITRATE
I have not led you through the desert in vain. Citrate has binding sites for calcium and will tend to bind on the surface of the terrace. But the molecule is large, and will stick up from the surface. Steps grow along the terrace. As they do so citrate molecules will disturb their advance. Instead of a new oxalate, bonds will form with an anchored citrate. This prevents the step from growing and therefore from increasing its radius in the direction of the citrate – it will bulge around the citrate but be stopped along the path blocked by the citrate.
When the density of citrate molecules becomes large enough to block length increase of a step, that part of the crystal is unable to grow despite solution supersaturation.
Not only can citrate produce ‘step pinning’ – but also it can bind to the kink sites on a step – the most active part where bonds are most minimal – and reduce the apparent growth kinetic constant.
WHAT CITRATE DOES
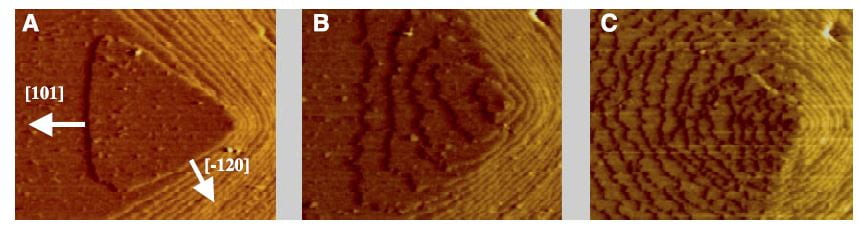
The lovely three part plate featured in this post shows by atomic force microscopy what citrate does to a calcium oxalate crystal. In the left hand panel, is the normal crystal just at the moment citrate was introduced at 0.02 the molarity of calcium, in a system in which the molarities of calcium and oxalate were equal. Noted are two crystallographic ‘faces’, the 101 and -120. By 10 minutes, growth along the 101 face, 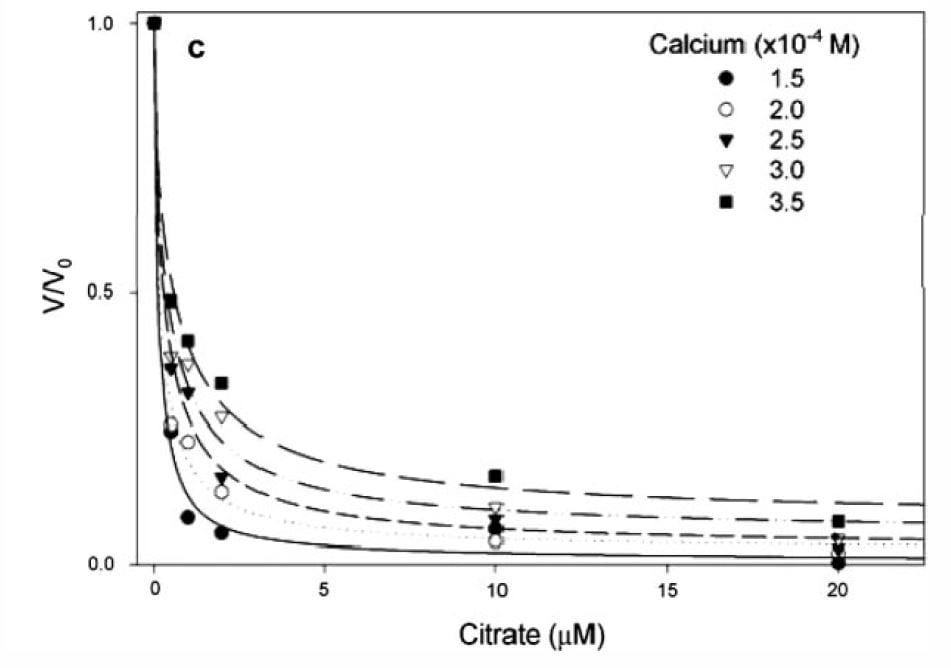 which is normally faster than the -120 face, has been slowed long enough that the shape of the growth hillock is rounded – the widths become similar.
which is normally faster than the -120 face, has been slowed long enough that the shape of the growth hillock is rounded – the widths become similar.
If you measure the growth of plates and express the ratio of the growth rate velocity to that in the absence of citrate (y axis of the graph at left) the ratio falls steeply as citrate molarity increases (x axis of graph).
The calcium molarities for each of the 5 different symbols range about 100 umol/liter, whereas the citrate molarities needed to reduce growth velocity by 1/2 are all about 1 – 2 umol/liter, far below the value which would alter calcium concentration via binding and thereby affect supersaturation. Therefore the effect is almost purely from adsorption on to the crystal.
In human urine, citrate and calcium molarities are in the range of 1000 to 6000 umol/liter, and the citrate calcium difference ranges around 1000 to 2000 umol/liter
The lines fitting the data are from the G-T relationship, supporting the power of the model to predict what happens in the real world, and therefore supporting the truth of the mathematics behind the calculations.
OSTEOPONTIN (OPN)
As though I have lost my senses, the name appears of a large protein and anyone with sense should wonder why. Is it not enough to have coped with citrate? Urine has numerous inhibitors of which OPN is but one. But, OPN has been studied well using the methods current in this article, so what better moment to introduce one of the great urine protein molecular inhibitors than when readers – if I have any left by now – 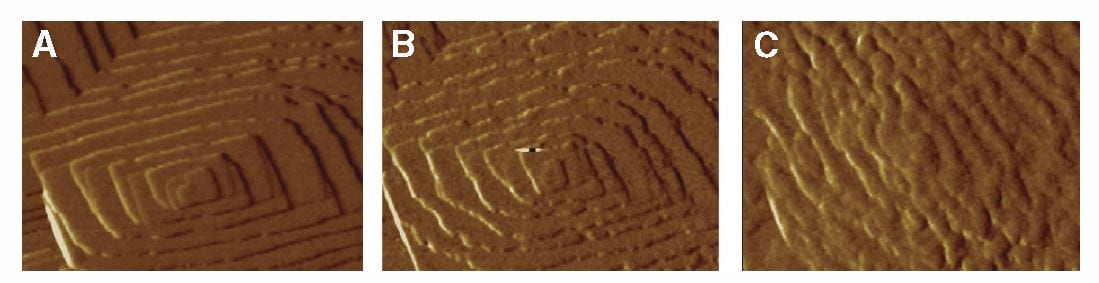 have had the stage prepared for its grand entrance.
have had the stage prepared for its grand entrance.
The left panel shows the by now familiar growth steps on a hillock of calcium oxalate. Addition of OPN at 0.005 umol/liter, far below the concentration of citrate that inhibits, made the steps blurred and slowed growth by 40 and 70 minutes (middle and right side panels). This is superficially like what citrate does. But the side of the crystal affected was not the 101 but the 010 direction. This cannot be seen in the picture.
This face specific effect of OPN vs. citrate suggests that the two molecules should exert a synergistic inhibition effect when both are present at the same time, and that is the case.
THE LARGER STORY
So far it is as if calcium oxalate were alone, forming and growing or not in sway to the forces of supersaturation and inhibition as a sailing ship to the wind and countervailing currents. Such a splendid isolation may be the reality in stone formers, or not. Other crystals are often present, brushite and apatite as special examples, and a serious if still unproved view of things holds that the three crystals engage in what I might call a specialized form of cannibalism, one in which citrate and osteocalcin (not OPN) play a role.
Brushite (BR)
Although it is not the most stable of the phosphate crystals, human urine is frequently supersaturated with respect to brushite (calcium monohydrogen phosphate) and, unlike calcium oxalate which forms de novo only at very high supersaturations, brushite forms readily at even low values of supersaturation and is not rare in human stones.
Of greater interest, perhaps, is that at least in simplified systems brushite can act as a local source of high calcium concentration to foster calcium oxalate and apatite crystals.
What I have to tell is a story which is utterly true and yet, in relation to human stones, utterly untested. It is compelling enough we should study the proposition in patients, although it might be difficult.
CALCIUM OXALATE GROWS ON BR
In a constant composition system that has a supersaturation for BR and calcium 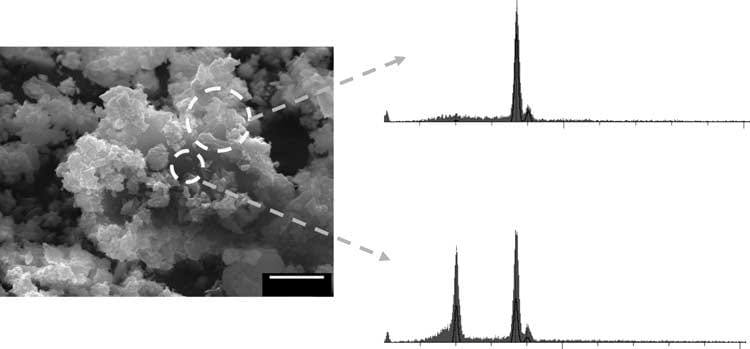 oxalate, calcium oxalate crystals are found (upper trace shows calcium without phosphate) on brushite crystals (lower trace shows calcium and phosphate signals from brushite below the overgrowths seen through the surface void).
oxalate, calcium oxalate crystals are found (upper trace shows calcium without phosphate) on brushite crystals (lower trace shows calcium and phosphate signals from brushite below the overgrowths seen through the surface void).
Of course, this is not urine, with its complex proteome. Thus far I know of no proof that this overgrowth phenomenon occurs there. The mechanism appears to be simple. Oxalate at the brushite surface has a higher affinity for calcium than does the phosphate in the BR crystal, and therefore calcium oxalate begins to form at the expense of the BR. One can observe dissolution pits on the BR surfaces where the calcium oxalate has essentially dissolved the BR crystal.
Of importance, no evidence supports the idea that the calcium oxalate crystals form directly on the BR surface. Instead it is as if the brushite serves as a highly concentrated local source of calcium ions so that calcium oxalate precipitates and BR dissolves in a local region of the solution leaving the calcium oxalate crystals to deposit randomly on the BR surface as was observed.
CITRATE INHIBITS THE SYSTEM
In this system, a modest supersaturation initiates BR nucleation by about 1400 minutes whereupon calcium oxalate begins to form 100 – 120 minutes later. Citrate added at 50 umol/liter delayed the onset of BR formation to 2900 minutes and increased the delay to 220 minutes before calcium oxalate appeared thereafter. This makes citrate a powerful inhibitor indeed, at least as studied in simplified systems.
HYDROXYAPATITE (HA) GROWS ON BR
In an undersaturated solution that contains osteocalcin, BR can dissolve and  reprecipitate as HA. The left panel shows osteocalcin coating steps on a BR crystal (left panel, white arrows point to protein on steps). Hexagonal HA crystals can be found on the surface (Right panel) also coated with osteocalcin (small dots on the surface).
reprecipitate as HA. The left panel shows osteocalcin coating steps on a BR crystal (left panel, white arrows point to protein on steps). Hexagonal HA crystals can be found on the surface (Right panel) also coated with osteocalcin (small dots on the surface).
The theory holds that osteocalcin on steps reacts with calcium and phosphate ions as they leave the step edges and that osteocalcin acts as a template for HA crystal formation because the spacing of gamma carboxy glutamic acid (Gla) residues in the molecule match the ordering for HA.
What the BR surface itself contributes is not clear. The HA is not oriented epitaxially on the BR surface – the patterns of charges do not match. In fact, the new HA crystals are randomly oriented. The authors of the review from which I have redacted this precis suggest the surface acts to aggregate the newly forming HA crystals. In other words, the case for HA is like that for calcium oxalate forming near BR crystals: dissolution and reprecipitation with new crystals depositing and perhaps aggregating on the BR surface. But the HA process differs in requiring osteocalcin, which acts, perhaps, as a templating intermediary.
A FINAL WORD
Being a calcium binding molecule, and a molecule that can specifically inhibit growth of both brushite and calcium oxalate, citrate has a unique potential as a crystal retardant in human urine. Its molarity comes close to that of calcium, so calcium binding can be considerable and therefore lower supersaturations. It acts as an inhibitor at an order of magnitude lower concentration than that present in urine so there is a great excess of citrate even when crystallization is itself considerable.
Given all this, its effectiveness to reduce new calcium stone formation is not a surprise but rather an experimental confirmation of a prediction that could well have arisen from more basic science. In fact, the clinical trials of citrate were made when that basic science was in its earlier phases.
This illustrates how the common paradigm of translational research – discovery, clinical application – lacks a proper subtlety. Discovery of promising properties and practical tests of efficacy can be in parallel, as in this case, and the outcome a durable science based not only on its own results but on proof of an important utile contribution to medical practice.
Regards, Fred Coe

Interesting article. It helps to understand how potassium citrate works
Thanks, Kim. The topic worried me a bit, being so technical, but people seem to find it useful to them. Great! Fred
Fred —
This explains a great deal and is enormously helpful. Thank you for taking the time to write these periodic notes. It is also a great reminder to keep pushing water and keep on track with my Urocit-K.
Regards — Susan.
Thank you for your kind remark, Susan. I am glad the site is useful for you. Regards, Fred
Hi Fred,
I don’t understand, if Citrate raises urine pH isn’t that a bad thing for calcium phosphate stone formers? It seems counter intuitive. If it is still the best way to prevent calcium phosphate stones, where can I get some?
Thanks,
Joe
Hi Joe, You are a very perceptive reader indeed. On the one hand the citrate salts can raise urine citrate and citrate binds calcium – lowering supersaturations – and inhibits crystal growth. On the other hand the potassium citrate is an alkali load which raises urine pH and that increases the supersaturation of calcium phosphate. That is the reason I pointed out that we need a trial of potassium citrate for calcium phosphate stone formers and while we are waiting physicians need to be cautious about using the drug for those patients. I in fact do not. Fred Coe
I have taken potassium citrate and do make phosphate stones I will be in a trial!!!!!
Dear Laura, it is true there is no trial of potassium citrate in phosphate stone formers, and it is possible though unproven that in some cases this drug could shift stone forming toward phosphate stones. Being entirely untested as yet, and given that the basic science does not in this case predict what will happen – high pH vs. calcium binding and inhibition – every physician has to make a personal choice. My choice is to get a trial sooner than later. Best, Fred Coe
Thank you once again for clearing up so many things. I never could tolerate potassium citrate and later on when my doctor realized I make phosphate stones I asked if I could off and when I asked if I should go back on and tolerate them he said no it is not needed. Please keep us posted about the trial.
Hi Laura, The trial I spoke of is what I want; no one has so far organized one. It is a large undertaking and trials are not my special favorite as a researcher. Regards, Fred Coe
Rather than take potassium citrate, I much prefer just to make sure everything I drink has lemon or lime slices in it, or both. Everything except milk and coffee. 😉 Don’t know if this will help in my situation, or not. Been doing this since late last year after having a SWL to break a lot of stones in my right kidney. Since then I have gotten a 9mm stone obstructing my right ureter. So what gives? I just don’t even know what to do now.
Hi Robert, First, is this a new stone or passage of a retained fragment? Second, be sure and get it analysed. Third, be sure you have covered all the bases in stone evaluation – take a look at this. Prevention is not hard but it is more line engineering than most areas of medicine. Once you have all the problems in hand, you fix them and then new stones will generally cease or slow a lot. Frankly this episode sounds like a prior or leftover stone passing now. Your physicians can tell you. Regards, Fred Coe
Hi Dr Coe,
I am a brushite stone former with a high PH and also want to protect my bones. I was planning on taking one hydroxy-citrate supplement (500mg garcinia cambogia providing 250mg hydroxycitric acid (HCA) or the supercitrimax pill with 450 HCA mg and 100mcg of chromium) once a day while practicing my low sodium, high calcium diet with no other meds. I don’t know the status of the trials and there may not be enough evidence for many years. Wondering if you would be willing to share your thoughts on these given your relationship with colleagues performing the trial and your broad knowledge of kidney stone prevention. Secondly, wondering if citrate in HCA and potassium citrate reduces calcium available to bone. I want the citrate to bind to my urine calcium but not to the calcium available to my bones before it is excreted in urine. Do citrate supplements such as HCA and potassium citrate leave less calcium for bones? Or rather do they just bind excreted urine calcium? I respect your time and consideration and greatly appreciate all you do! Thank you!
Hi Traci, I presume your urine calcium is high, and that your bone disease is ascribed to hypercalciuria and not menopause. If so, low sodium high calcium diet is a good idea, but if bone mineral loss continues your physicians may want to add additional meds to protect against fractures. You must use 24 hour urines to monitor urine calcium when you use high calcium diets and be sure diet sodium is low enough. As for HCA it is available from grocery stores. It may be helpful, is certainly not a problem, and why not use it? Check with your physician! As for chromium, I know nothing at all. Citrates are metabolized, HCA appears in urine and I know of no reason that it would prevent calcium absorption. You might want to take it away from meals, however. There are several safety studies of potassium hydroxycitrate, here is one. Regards, Fred Coe
I should have mentioned I just started menopause this year. I had a dexa and it showed t scores ranging from -.5 (neck) -.3 (spine) to .1 (hip) and z-scores ranging from .2 to .6. It says I am “normal” so I think those are good results. Surprising it is “normal” as before this diet, I embarrassingly made no effort to get calcium and I was probably only getting about 300mg/day – not sure what I was thinking?! I want to ensure my bones do not decline so now I am consciously consuming 1000 mg calcium a day. My previous test in October when I increased calcium to 700mg day showed urine calcium of 303 with a sodium score of 100. After that test, I boosted my calcium to 1000/mg day and reduced sodium to 1000mg day. I will get a new 24 hour urine test soon. I am scared my urine calcium will not really change since the added diet calcium will probably just offset my improvements to sodium. Do you think I will see a reduction in my urine calcium? Sorry to burden you with this. I appreciate your kindness and thoughts. I am considering traveling from a neighboring state to U of Chicago for care. Extremely impressed with U of Chicago’s comprehensive kidney stone program and this website.
Hi Traci, The higher diet calcium – to US recommended levels – is only a good thing if diet sodium is low enough to keep the calcium out of the urine. Your sodium goal of 1000 mg is very ambitious, but if you achieve that I imagine your urine calcium will be a bit lower than when you ate little calcium and – as a bonus- your urine oxalate will fall to very low levels. The real trick of low sodium high calcium diet is low urine oxalate and bone protection. See what your new 24 hour urine shows. Regards, Fred Coe
Dr. Coe,
I was a resident at UC many years ago and remember fondly “working out” cases with you at Morning Report. I frequently turn to this site to help teach our endocrine fellows about stone formation. Invariably, I chuckle as I learn. Thank your for developing this site and infusing it with your singular wisdom and wit!
Hi Varman, Much thanks. I am thrilled that it is useful. Warm regards, Fred