 Elder Joseph Brackett, a member of the Shaker community at Sabbathday Lake, wrote ‘Simple Gifts‘ in 1848. Although properly classified as a song (Shaker music was usually classified as anthem, hymn, or song), scholars believe it was a ‘dancing song’, or quick dance. Aaron Copeland offered it to the whole world in his ‘Appalachian Spring’ ballet and collection of ‘Old American Songs set for voice and piano’. He did not know its history, but his music reveals the powerful heartbeat of a dance inside the gentle melody of this beautiful Shaker song.
Elder Joseph Brackett, a member of the Shaker community at Sabbathday Lake, wrote ‘Simple Gifts‘ in 1848. Although properly classified as a song (Shaker music was usually classified as anthem, hymn, or song), scholars believe it was a ‘dancing song’, or quick dance. Aaron Copeland offered it to the whole world in his ‘Appalachian Spring’ ballet and collection of ‘Old American Songs set for voice and piano’. He did not know its history, but his music reveals the powerful heartbeat of a dance inside the gentle melody of this beautiful Shaker song.
The simple poetry celebrates the idea of a middle place, ‘the place just right’, which is the nature of a valley, a place of ‘love and delight’: A place between. Aristotle’s vision of the mean between extremes is perhaps a more sophisticated vision of such a place, and is said by experts to have itself arisen in part from medicine. His subtle vision, not at all quantitative, is perhaps best symbolized not by arithmetic or black and white extremes with a middle path between, but by the archer who places an arrow within the bull’s eye, the center of the target, allowing for the wind, but not too much, for the distance, and – crucially – recognizing that the center is itself not a point but a desired region.
Which brings me to my topic here, which is about a middle place that is not so easy to define yet absolutely definable if you work at it.
I have worked to define it for you because it is an essential part of kidney stone disease, and a part not well nor often enough spoken about.
It is a story of failure in that my nearly 5 decades in research our whole community has not been able to make enough progress to being new tests or treatments for physicians and patients. But the story also contains some gleam of possibility bright enough to lure me back to papers we wrote nearly 20 years ago.
If you read this, if you stay with it, it will reward you with some surprises and perhaps a glance at the odd and uncanny ways of nature.
The Purposes of the Kidneys
Being as we are, preoccupied with prevention of kidney stone crystals and therefore of kidney stones, we can forget sometimes why the problem is so common as it is. Above all, since we  left the sea, our kind has been in perpetual search of enough water and salt to maintain our inner sea – much like the oceans we grew up in – within its natural boundaries, among which are the concentrations of sodium and calcium.
left the sea, our kind has been in perpetual search of enough water and salt to maintain our inner sea – much like the oceans we grew up in – within its natural boundaries, among which are the concentrations of sodium and calcium.
To this end, our kidneys are primed to conserve water and sodium to an outer extreme if necessary, so our needs for both can be fitted to their availability. In this, calcium required a most special kind of treatment. On the one hand we have calcium phosphate skeletons which are forever renewed by a bone turnover process in which calcium salts are liberated and reformed into new crystals. On the other, we have diets which supply varying amounts of calcium to enter the blood with each meal.
In the middle, we have the blood calcium. It must produce, along with the blood phosphate, a sufficient supersaturation to permit new bone crystals to form. That is a physical necessity and determined by the evolutionary ‘choices’ that produced a hydroxyapatite crystal skeleton. Blood calcium concentration  must be very stable, because that same evolution has selected it as a key signaller for heart and brain cells, kidney cells, bone cells, and probably all cells.
must be very stable, because that same evolution has selected it as a key signaller for heart and brain cells, kidney cells, bone cells, and probably all cells.
Yet such stability must be maintained in an open system that permits food calcium in at random rates determined by habit, choice, accident, and society, and such an open system must control the ingress and egress if blood calcium is to be very stable.
It is because of these complexities we encounter significant amounts of calcium in the urine along with a urine volume which can vary from one half to eight or ten liters daily.
Phosphate also is part of an open system, less perfectly regulated, so the urine is perpetually at risk for that same kind of calcium phosphate supersaturation as is needed in blood, even greater because water can be conserved just when calcium needs to be removed, the two processes being independent of each other.
Oxalate is an unfortunate metabolic waste product which forms very insoluble crystals with calcium. It adds the final dimension, a risk of calcium oxalate stones.
The result is, if one pursues my original metaphor, one of the two mountains. The needs of the blood and the evolutionary ‘choice’ of an open system must result in combinations of water and mineral balance which produce risk of supersaturation of the urine with calcium salts, and do so variably in the course of life. This risk entrained by our biology and is inescapable.
The Appearance of Protection
If urine was a simple solution, supersaturation would produce crystals all the time, in an uncontrolled way, and it is likely that the kidneys as we know them would not have fitted our species for success in the competition to survive. But urine is not a simple solution. It is filled with retardants of crystal formation. This large and perhaps random assortment of molecules, as well as certain small ones such as citrate and inorganic pyrophosphate, permits us to form stable supersaturated urine and yet remain, as a species, reasonably free of stones.
Inside the Ostwald Limit
Long ago, as I measure the life of this website, I called attention to a wonderful article about saturation. Here is the key figure from that article. Temperature is on the vertical axis. On the horizontal axis is what amounts to the concentration of some material in some solvent. For us, it is the concentration of, as an example, one of the stone forming salts like calcium oxalate in urine – essentially water.
Any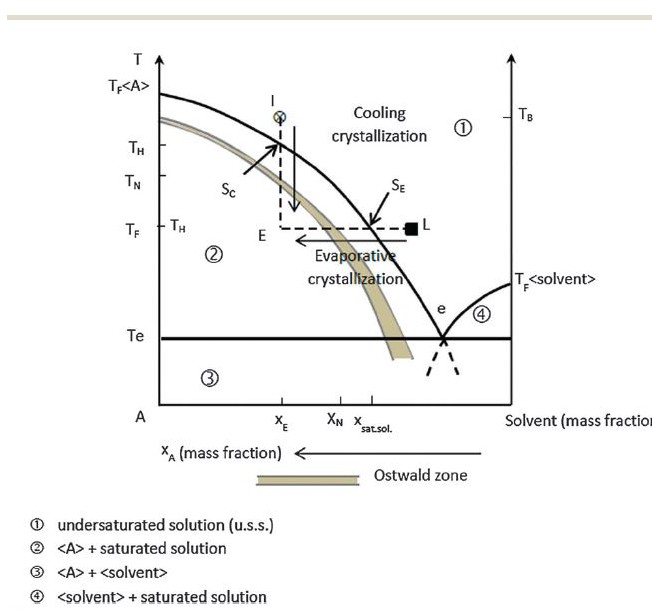 urine or solution can be undersaturated – the concentration of a stone forming salt like calcium oxalate is below its solubility (Region 1). Crystals will dissolve.
urine or solution can be undersaturated – the concentration of a stone forming salt like calcium oxalate is below its solubility (Region 1). Crystals will dissolve.
The solid curving line is the solubility. Stir sugar into water; no matter how long you stir, how much sugar is at the bottom of the glass, only so much will dissolve.
As in the experiment with sugar and water, when you heat the water, more of the crystals you stirred in will dissolve. Thus the solubility curve shifts to the left – more dissolved salts – as the temperature (vertical axis) rises (the way the graph is made increasing concentrations of salts are to the left!).
When the water cools to room temperature, the ‘extra’ sugar, which means sugar dissolved at a concentration above its solubility at room temperature, produces supersaturation. You can follow the vertical line from ‘x’ down to ‘E’ which shows how cooling moves the concentration from undersaturation to extreme supersaturation.
But, crystals need not form if you did it just right.
If you produced a supersaturation, but not too much of one, crystals are ultimately inevitable but not necessarily there right away. If you produced too much of a supersaturation, they will form immediately.
The demarcator between these two states is called the Ostwald limit, which is actually not so much a line as a band which is referred to at the Ostwald zone – like aristotle’s bulls eye, not a point but a region or place.
Below the Ostwald limit (or zone, the words are interchangeable) but above the line of solubility in the graph (Region between the solid curving line and the Ostwald limit) is the zone of metastable supersaturation: Energy is stored in the solution, crystals can form, but they are in abeyance.
Such a sugar solution is not very stable. Tap the glass with a spoon, or shake the solution, and it will probably crystallize.
Kidneys do not change temperature – everything in the body is at 37 degrees centigrade. Instead, they remove water from the urine to conserve it for the body, and raise the saturation as evaporation will – movement along the horizontal direction on the graph labelled ‘evaporative crystallization’.
Urine is usually in the metastable supersaturation zone with respect to calcium oxalate and calcium phosphate, between the solid line of solubility and the menacing Ostwald limit.
Yet it is also very stable. You can shake it, leave it out in a room for a few days, transport it a thousand miles to a laboratory, yet little of its calcium and oxalate will leave the solution. The zone of metastable supersaturation is wide and we generally form urine within it.
Above the Ostwald zone (Region 2) crystallization is rapid and uncontrollable. We see patients sometimes whose urine is milky from heavy calcium phosphate precipitates. Uric acid can shower down as orange red gravel. Rarely, and usually because of incomplete prophylaxis before treatment of hematopoietic malignancies, massive uric acid crystalluria can plug terminal collecting ducts and cause acute renal failure, or plug both ureters with the same result.
Why is the Ostwald Limit there?
One would think that as supersaturation rose crystal formation would proceed pari passu, but no. You must raise concentrations until the supersaturation reaches the limit of metastability – the Ostwald zone – and even beyond. Because of the biology I have already presented, a biology of the flow of calcium and phosphate through an open system which also conserves water, such supersaturations can occur at random depending on all the factors of life which affect diet and fluid intake.
But even this is not really a sufficient explanation: Why is the upper limit there? What creates it?
Consider a seawall, as in Holland, perhaps.
Like the waves of the sea, flows of mineral and tubule fluid create waves of supersaturation, invisible and unheard, but physically powerful. As the waves push against and break on the seawall, these waves of supersaturation encounter the Ostwald Zone, they cannot break through into formation of a solid phase.
They cannot for two reasons.
The first is that nucleation poses an energy barrier. Molecules of oxalate or phosphate will attract calcium atoms to form the complex structure of a crystal, but random thermal agitation disperses pairs as they form. So everything depends on chance. If a pair manage to attract some partners, the energy of their bonds may become strong enough to hold despite thermal agitation. Let a few lucky clusters gather in more friends and the cluster can remain stable. So random motion is like the seawall: waves of saturation come and disperse, leaving no trace behind. One might say there is a free energy of formation for crystals: One needs to provide enough compaction to offset thermal dispersion.
This need to overcome an energy barrier is universal for crystals, and is why there is always an Ostwald zone and a region of metastability.
Perhaps because the waves are fierce in kidneys, evolution has provided another layer to raise the wall, to advance the Ostwald limit further from the saturation line than might be the case for a simple solution.
Citrate, inorganic pyrophosphate, and at least some of the vast urine proteome interfere with the additions of atoms or molecules onto a promising cluster. Being highly charged, they add onto the growing crystals as calcium or oxalate or phosphate might. But, being of the wrong size and shape, they interfere with the orderly creation of a crystal and retard crystal formation. Flow through the kidney is continuous, so to retard crystallization is to make it irrelevant to kidneys and therefore to us.
Locating the Ostwald Limit
But where is any one person, at any one time, within the metastable limit – inside the inner boundary of the Ostwald Zone: At the high extreme of metastability, in the middle, or at the low end?
It matters. If at the high end, we are at risk, for a minor perturbation of fluid intake or from food can send us beyond the limit into the zone of immediate spontaneous nucleation. That is not where we want to be.
To find the limit for a urine sample we have to raise the saturation and determine when crystals form. We do this by adding calcium, to make calcium phosphate crystals, or oxalate to make calcium oxalate crystals. The supersaturation at the point of crystal formation is beyond the Ostwald zone, for that urine: above the upper limit of metastability.
These two terms mean the same thing: The experimentally measured upper limit of metastability (ULM for short) is the actual supersaturation of a particular urine – or any other solution – at the Ostwald limit. The former, ULM, is an experimentally measured supersaturation. The Ostwald limit, or zone, is a theoretical concept applicable to all solutions.
If the original supersaturation of the urine is compared to the ULM the distance between the two is a measure of safety or peril. Essentially, if we need to add calcium or oxalate to make crystals, the urine supersaturation is below the ULM. The distance between the supersaturation and the ULM is a measure of how safe one is, how much ‘room’ is left for more saturation before crystals become inevitable.
Being so important as it is one might imagine the ULM is measured all the time, but it is not because the measurement is impractical to produce commercially.
I know.
In my earlier life I founded Litholink Corporation, and was chairman of the board for 11 years. During that time we wanted to create a ULM measurement for sale, and could not.
The Upper Limits of Metastability (ULM)
How do we really measure the ULM?
Charles Pak, who contributed so much to citrate as a treatment, provided the measurement we used. A 24 hour urine is divided up in many transparent tubes, to which we add increasing amounts of calcium (to get the CaP ULM) or oxalate (to get the CaOx ULM). After adding, we read the tubes at 3 hours and note the tube which had the lowest amount of added calcium or oxalate yet had become cloudy. The supersaturation of that tube is calculated from how much was added along with all the measurements which were made before anything was added, and that supersaturation is the ULM.
There is one more small but probably critical detail. For the CaP ULM, the one we get by adding calcium, we bring the pH to 6.4, a single standard level. If pH is too low (acid urine) CaP crystals will form only with vast additions of calcium because most of the phosphate is in the single charged (monovalent) form which does not combine with calcium. However the raising of pH introduces an odd effect. The ULM measurement is independent of the original pH of the urine, whereas the original supersaturation of the urine is not, so the ULM – SS distance, which we have been speaking about as a critical measure of risk, must be dependent on the urine pH as we measure things, but might not be if we measured the ULM at the actual pH of the urine.
Measurements of ULM and SS in Men
WHAT WE FOUND
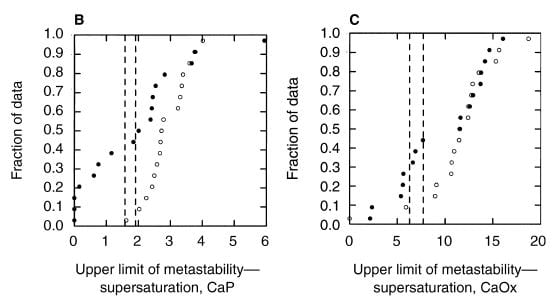
A paper by me, John Asplin, and others illustrates the ULM and makes a point of some worth. Among 17 normal men, the ULM – SS distance for CaP ranges from 1.5 to 4 (open points on the left panel) whereas values for 17 age matched calcium oxalate stone formers (left panel filled circles) range from 0 (spontaneous crystallization before adding extra calcium) to 4, with only 4 points matching the normal distribution. The dashed lines are down 1.5 and 2 SD from the mean of the normal values. Patients have a much lower ULM – SS distance than normal people. They are nearer to the brink.
For calcium oxalate (right panel), the patients split into two groups: About half show values that match the normals, the other half are considerably below.
WHAT IT MEANS
Consider that all these patients formed calcium oxalate stones. Likewise that the ULM – SS distance is a measure of the headroom between prevailing supersaturation and the Ostwald Zone for a given urine. The data would imply that having a smaller margin for CaP somehow increases risk of calcium oxalate stones, whereas the ULM – SS distance for calcium oxalate itself is far less robust in distinguishing between stone formers and normal men and therefore less evident as a risk factor.
Why should this be? The stones are calcium oxalate, not CaP.
At the time, we were not sure, but now we have considerable reason to believe what we found in 1999 was prescient.
Calcium oxalate stones often, perhaps always form over CaP crystals that are themselves embedded in the kidney tissues. These embedded crystals are CaP in the form of hydroxyapatite, which is found in tiny amounts in most calcium oxalate stones and is the residue of how the stone formed in the first place.
It would appear that the embedded crystals, which are called Randall’s plaque after the name of the man who first described them, lie just below the outer lining of the renal papilla, the terminal part of the kidney from which urine leaves to enter the urinary tract. If that lining is breached, urine comes up against the plaque, and a base of apatite forms over which calcium oxalate eventually creates a stone.
The link will take you to an article by Dr Andrew Evan which shows the whole process and even includes a movie of how this area looks as seen in the operating room during kidney stone surgery.
Being the first step in the process, formation of the initial CaP stone base on denuded plaque is critical for calcium oxalate stones, and therefore a greater propensity for CaP to form – a reduced ULM – SS distance – is a key risk for such stones to form.
WHY NOT THE CALCIUM OXALATE ULM – SS DISTANCE?
Even so, calcium oxalate is the main stone crystal so why is its ULM – SS distance not more important?
It is not so important because the Ostwald Zone applies to the initial formation of crystals.
Once crystals are formed, any supersaturation is enough to produce growth.
Elsewhere I have mentioned that crystals can serve as templates for each other, templates which promote the process of new crystal formation. Although more research is needed, I suspect that once formed the apatite base somehow promotes the calcium oxalate overlay, so the magnitude of both the supersaturation and the ULM – SS distance for calcium oxalate become less important.
Our prior articles about supersaturation point out that urine SS with respect to calcium oxalate is always far above 1 – there is always supersaturation. The same is not true for CaP – normal people are often undersaturated so the average saturation for both male and female normals is just above 1 – the figures in the link show this point.
As a consequence, once a stone base forms, urine contains enough supersaturation to produce calcium oxalate over the base whether or not the ULM is above or near the supersaturation.
Measurements of ULM and SS in Women
Does this same thing happen in women?
It does.
In a second paper, concerning women with calcium 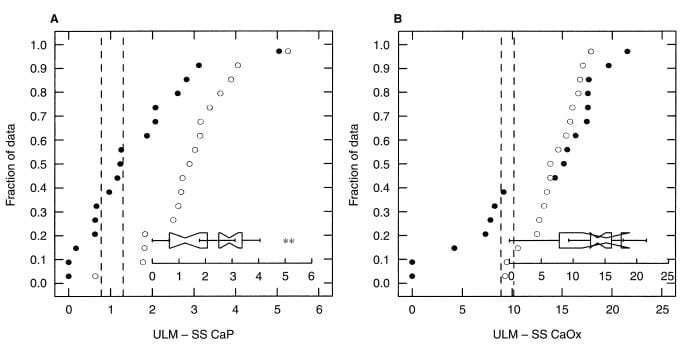 oxalate stones (black circles) the ULM – SS distance (left panel) is much smaller than among matched normal women. In fact the phenomenon is more marked and consistent than among men (compare this figure with the one above).
oxalate stones (black circles) the ULM – SS distance (left panel) is much smaller than among matched normal women. In fact the phenomenon is more marked and consistent than among men (compare this figure with the one above).
For calcium oxalate (right panel), likewise. Women are much as men, with some patients being low in their ULM – SS distance, others perfectly normal. The notched boxes are an extra; when the notches do not overlap the two sets of data are not likely to be the same statistically, as in the left panel, whereas in the right panel they do overlap meaning the two sets of data are not different.
What Controls the Upper Limit of Metastability?
An obvious answer is the vast mix of urine proteins. Among those proteins are known inhibitors of calcium crystal formation and growth, so why not assume this presently unexplored trove plays the main role and wait for modern proteomic techniques to clarify matters?
Citrate
I would have agreed, but decided that in the mean time, while we wait for new proteomic science, one might look at smaller molecules. 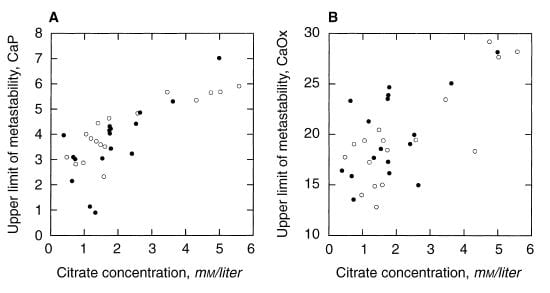 One reason for that decision is that we did just that decades ago, found a possible candidate, and perhaps did not pay enough attention to our own work.
One reason for that decision is that we did just that decades ago, found a possible candidate, and perhaps did not pay enough attention to our own work.
Among men, the ULM for CaP, which is shown in the left panel, clearly varies with the concentration of citrate in the urine. Moreover, it does so in patients (black circles) and normal men alike. For calcium oxalate (right panel) the relationship is not so clear. As I look at the CaP ULM data the very low ULM values at the lower left of the left panel, mostly are in urine with low citrate concentrations.
About the same pattern occurred in women.
We had changed our figure style between the two papers by adding the ellipses so I should explain them.
They are empirical shapes designed in this case to contain 68% of the data. Their elongation is a crude visual measure of how well, in this case, ULM and citrate concentration ‘correlate’, literally co – relate, change in parallel with one another. The tilt is an index of how much one changes as the other one changes.
The normal women, open circles in the dashed line ellipse, show a very strong correlation between CaP ULM and citrate concentration, and the same for the patients (Left panel). Once again, the lower ULM values tend to be in the lower ranges for citrate. The scales on the horizontal axis are logarithmic – plotted as logarithms to the base 10 – as a way of spreading out the lower values and accommodating their wide range.
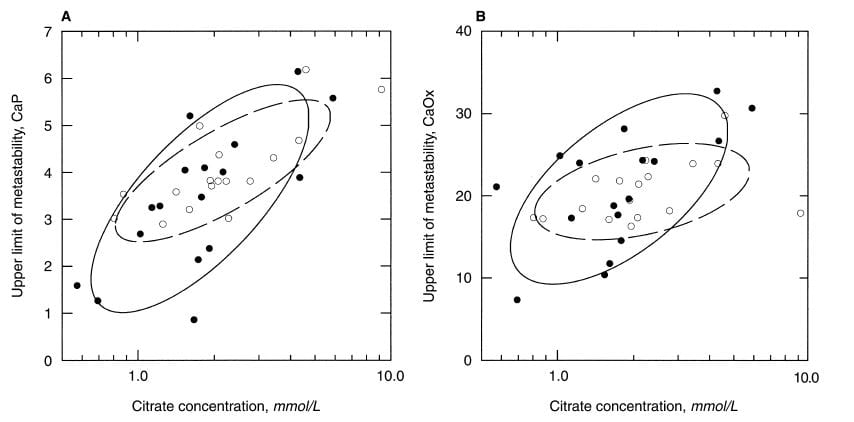 For calcium oxalate ULM (right panel) patients show a strong correlation, normals less of one, so there is more variability than for CaP.
For calcium oxalate ULM (right panel) patients show a strong correlation, normals less of one, so there is more variability than for CaP.
When we wrote the papers, John Asplin and I realized that citrate concentration was a powerful correlate of the CaP ULM, and looking back on the two papers, and in the context of all we have said about citrate as a calcium binder and crystal inhibitor on this site, I am once again struck by the possibility that citrate almost certainly plays a main role.
Correlation and Cause
Because I may be forgiven for any degree of academic intensity, being a professor, I pause here a moment to reflect on the meaning of correlations with regard to cause, the latter a vexed word at best.
In this article I mean by ’cause’ that citrate may itself, as a molecule, specifically retard crystallization enough to affect the measurements we make. No more.
If citrate concentration were not at all correlated with the measured ULM such a proposition would be false, because a molecule which alters the ULM at one concentration should alter it at another concentration and being a presumed inhibitor the direction should be an increase in the ULM as the concentration goes up. That we found the correlation does not prove citrate is a cause of the ULM, but at least it means the idea is not obviously false.
Can Citrate Raise the ULM for CaP?
DIRECT ADDITIONS OF CITRATE TO URINE
The only way to prove causality is to do something more direct than establish correlations exist, which we did some years ago by adding citrate to urine and measuring the ULM.
The idea was to take urine samples, measure the CaP ULM – the one of higher importance and the one that correlates with urine citrate concentration – and add citrate with repeated 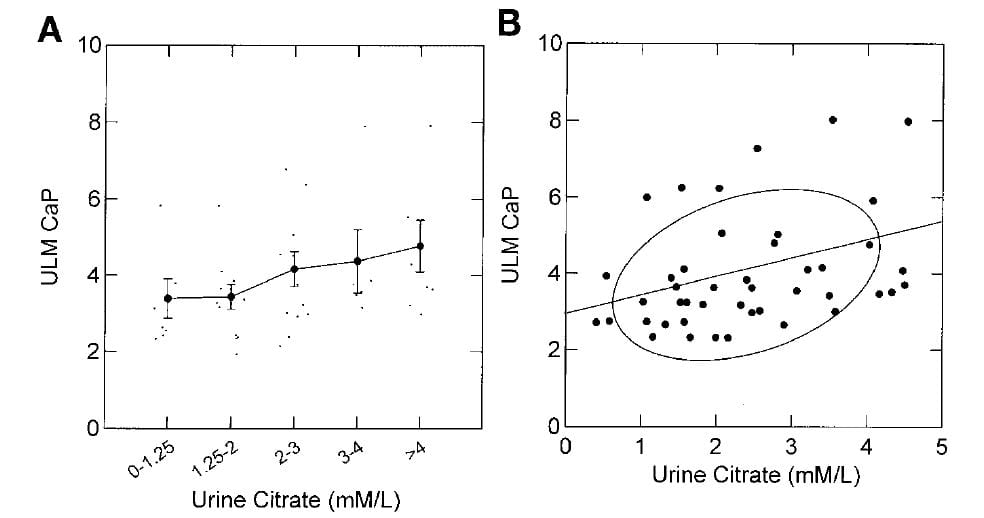 measurements asking if the higher urine citrate concentration raised it.
measurements asking if the higher urine citrate concentration raised it.
It did.
The ULM measured by adding calcium to aliquots of the urine samples at a fixed pH of 6.4 (a technical convenience in the assay already mentioned) rose as the citrate concentration of the samples was increased.
The effect was modest as can be seen by the small increases of ULM as one goes from the lowest to highest citrate pentiles along the x axis of the left panel, and by the modest slope of the ULM on urine citrate concentration shown in the right panel (0.4 units of ULM /1 mmol/l of citrate increase).
In another experiment, the ULM was achieved not by adding calcium, as is conventional, but by raising pH. As the urine is made more alkaline, a higher proportion of phosphate is in the divalent (2 negative charges) state which permits it to combine with calcium.
In those experiments, the citrate effect as judged from the slope of ULM on citrate concentration was not different from when calcium was added (not illustrated here). In other experiments urine phosphate concentration was increased at a constant pH of 6.4, so instead of increasing the proportion of phosphate available to combine with calcium we changed the total concentration of phosphate.
URINE PH HAS ITS OWN EFFECTS
Along the way, what with changing calcium, and phosphate, and pH, we made an observation which we did not predict.
As I 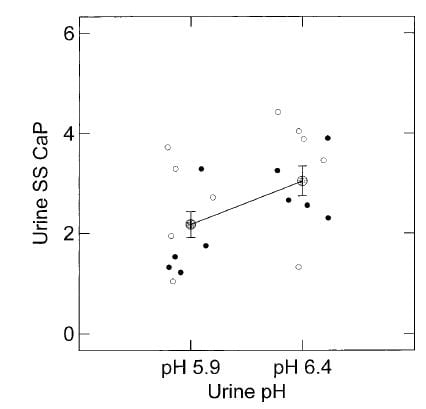 mentioned the effect of citrate on the ULM was more or less the same whether ULM was achieved with pH, or calcium, but – as a surprise – the ULM was higher at a higher pH – pH itself appeared to affect the ULM.
mentioned the effect of citrate on the ULM was more or less the same whether ULM was achieved with pH, or calcium, but – as a surprise – the ULM was higher at a higher pH – pH itself appeared to affect the ULM.
Here, the ULM was measured in the same samples by raising calcium or phosphate (open and closed circles, respectively) but at two different pH values, 5.9 and 6.4. Urine citrate was not changed. The ULM values from the two methods did not differ, as can be seen by their overlap, though the calcium points tended to be a bit higher. But at the higher pH the ULM itself was higher whichever way we measured it.
Because we calculate the supersaturation at the ULM accounting for such things as the proportion of phosphate in the divalent form, this pH effect is not simply arising from the simple physical chemistry. It is something else.
One possibility is that citrate is more effective as an inhibitor at the higher pH because it has more charge.
Citrate has 3 separate sites at which pH can affect its charge and the pH at which the third site is half saturated with protons, in other words half is free to bind to crystals, is indeed 6.4. Note that the binding of citrate to calcium in solution, which would of course affect the calculation of supersaturation, is already accounted for in the computer programs we use, so the effect of binding would be to the crystals: Binding to crystals in order to inhibit their growth.
OUR BEST ANSWER SO FAR
Given what I have so far shown, it is reasonable to say that urine citrate contributes to the ULM, and that in general higher concentrations of citrate will associate with and cause higher urine ULM for CaP. We did not do specific experiments on the ULM for calcium oxalate, as you have noticed, because it did not seem as important as that for CaP.
The Next Level
But more can be done to isolate factors which might be important.
Even though associations cannot prove causality they can point to possible ones, and we have not as yet explored all associations with the ULM.
To extend such observations, I put together all of the original data from both of the papers with John Asplin, so men and women stone formers and normals are in one file and associations can be sought across the sexes and with twice as many observations as when men and women are studied separately.
What to Do?
For those of you who are analysts of data, what I did is obvious, but for others who are not I thought a moment of explanation would be in order.
First of all, we are interested in the ULM for CaP, and want to know which measurements we have made correlate with that ULM; but we have made many measurements.
How does one proceed to ask about associations of many different measurements with the ULM?
Certain measurements are expected to affect the ULM CaP, the supersaturation at which a urine sample begins to crystallize – the Oswald limit: pH – because we already know it had an effect; volume – because all of those proteins we have mentioned as inhibitors will be presumably more concentrated when urine volume is lower so ULM might fall as urine volume rises; citrate – because we already know it has an effect; gender; whether a subject is a patient who forms stones or a normal; and the concentrations of the main constituents of calcium phosphate crystals: calcium and phosphate.
But these are a lot of measurements. How do we sort out their separate effects on the ULM?
The method has a fancy name – multivariable general linear modeling – but is a commonplace and friendly instrument much to my taste for this kind of work, carried out by computer programs – no one can compute this kind of thing by hand!
(For those of you with a bent for this work, I actually looked first at ALL of our measurements in a large stepwise model and chose out the ones with individual correlations to use here. I used SYSTAT™ GLM programs because I like their excellent graphics)
Correlations of Many Measurements with the CaP ULM
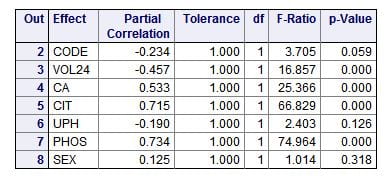 I asked our ‘friendly’ program how well each of our chosen measurements correlated with the CaP ULM, and it obligingly
I asked our ‘friendly’ program how well each of our chosen measurements correlated with the CaP ULM, and it obligingly
showed me the results.
Here they are.
The ‘partial correlations’ are just that: How much each measurement or trait varies with the CaP ULM independently of the other measurements or traits – therefore ‘partial’ correlation, correlation pertaining to that one ‘part’ of the ensemble of measurements or traits. Perfect variation gives a value of 1, a minus sign means as the measurement goes higher the ULM goes lower.
A glance will show you two outstanding correlations: citrate (CIT) and phosphate (PHOS) concentrations in the urine (0.715 and 0.734, respectively). The ‘F’ values (named for Sir Ronald Fisher) give an estimate of the weight or importance of each measurement in accounting for the total variation of the ULM. For an introduction to F values, I love this personal blog post. For a nice rigorous walk through, I like this one. It applies specifically to F tests in regression as we are doing here. The ‘p’ values are the probability that the correlation might have occurred by chance.
Stepwise Regression
We want to isolate which measurements ‘most matter’ and assess their value for understanding the ULM, and this involves ‘stepwise’ regression. The program ‘takes’ the leading measurement – largest F value – ‘out’ and shows its individual regression with the ULM. That measurement would be urine phosphate concentration because in the table just above it had the largest F value.
It then re-calculates the residual correlations for those remaining, as if the first were not there at all.
I do not clutter the page with each iteration, but simply say that urine citrate concentration came next, and after it was
 removed the remaining variables no longer had any significant correlations with the ULM and could be set aside.
removed the remaining variables no longer had any significant correlations with the ULM and could be set aside.
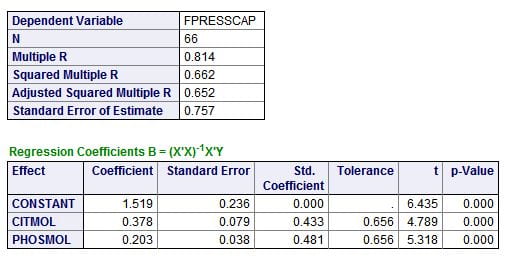
The result, summarized in the little tables to the left, bears some thought.
Citrate and phosphate concentrations both have about the same correlation with the CaP ULM. This is best seen in the standard (Std. Coefficients). A perfect correlation is 1, both are about 0.4 -0.5, about the same. Instead of F values, there are ‘t’ values which simply test how likely it is either is likely by chance; the p values are very low, meaning not likely at all.
The magnitudes of the effects are best estimated from the coefficients, which give the change in ULM for a unit change in citrate or phosphate concentration. Both are expressed here in their molarities – corrected for the different sizes of the two molecules. For every mmol/l of citrate change, ULM CaP rises 0.378 units; this is a lot like the 0.4 unit change we measured as we raised citrate concentrations in urine. For phosphate the effect is smaller, 0.2 units per mmol/l change.
The unpromising small box at the top is perhaps the most interesting. The overall correlation (regression is the more formal word) is 0.814, meaning – in a crude way – about 81% of the variability of the CaP ULM is related to (accounted for by) variations in urine citrate and phosphate concentrations. For reasons I do not want to go into here, this needs to be refined and corrected, which is the Adjusted Squared Multiple R showing that given the number of observations and individual regressions, 65.2% of the variation is probably related just to these two measurements.
What happened to being a stone former or not, and what happened to sex?
They both had no influence at all once these two measurements are taken into consideration.
What happened to the vast pool of urine proteins?
 Among them they may well account for only 35% of the variation in the CaP ULM.
Among them they may well account for only 35% of the variation in the CaP ULM.
How Can We ‘See’ the Combined Effects on ULM CaP
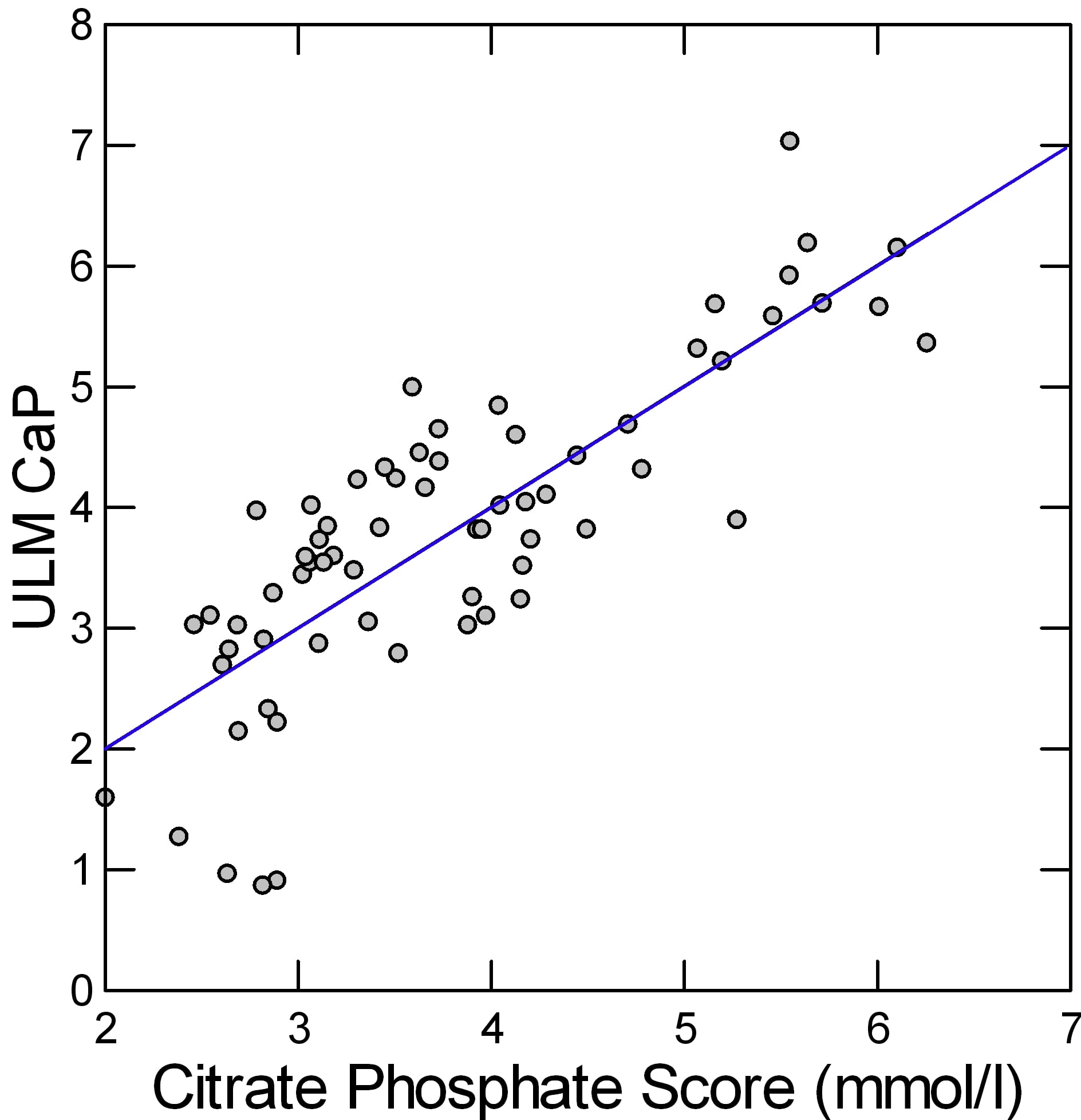
The two coefficients and the constant in the rectangle just above are the regression coefficients for the change in ULM CaP on citrate and phosphate, so we can make a simple linear equation as many of us did in 7th grade: ULM CaP = 1.519 + 0.378*urine citrate + 0.203*urine phosphate. This gives a kind of score or combine of both effects. A plot of the real ULM CaP (Y axis of the graph) against the score (X Axis) shows how well the pair correlate with the measured value.
The result looks pretty good. The linear regression of the ULM CaP on the score is plotted as a line. Since men and women, and patients and normals do not matter once these two measurements are considered, the points are all a uniform gray.
The regression of the ULM CaP on the score shows a remarkable fit: The slope is 1.001, meaning for 1 unit of change in the score – combined effects of citrate and phosphate – one gets 1 unit of change in the ULM.  When both are 0, the estimated value of the ULM CaP (constant in this table) is not different from 0. The overall impression is that these two simple molecules may – regression is not causality! – account for a very large amount of the ULM phenomenon in urine.
When both are 0, the estimated value of the ULM CaP (constant in this table) is not different from 0. The overall impression is that these two simple molecules may – regression is not causality! – account for a very large amount of the ULM phenomenon in urine.
How Can Citrate and Phosphate Control the CaP ULM?
Citrate
For citrate, the answer is easy. It is an established kinetic retardant of calcium crystallization.
We did experiments that showed citrate can raise the CaP ULM, but the effect was small. Here it seems of about the same magnitude.
We never tested the phosphate effect on the ULM, we simply used phosphate additions to achieve the ULM. In general higher urine citrate concentrations will be associated with higher urine pH so the pH effect we found in our experiments is probably part of the regression of the ULM on urine citrate and pH itself drops out as an independent force.
Inorganic Pyrophosphate (PPi)
The phosphate molecule alone is not a reasonable candidate for an effect on calcium phosphate crystallization as it is in  fact one of the components of the calcium phosphate crystal. But inorganic pyrophosphate, shown here as the di-sodium salt – can inhibit CaP crystal formation.
fact one of the components of the calcium phosphate crystal. But inorganic pyrophosphate, shown here as the di-sodium salt – can inhibit CaP crystal formation.
The molecule is simply two phosphates linked together through a common oxygen atom. From all we have said on this site, the two charged oxygens at the lower middle should look suspicious, able to find and bind to calcium atoms.
IT IS IN URINE
A recent review summarizes much of what is known about this molecule in bone and joints and urine. PPi strongly inhibits hydroxyapatite crystal formation and growth, so is an excellent candidate to raise the CaP ULM. Citrate and PPi seem synergistic with regard to HA inhibition. The molecule is produced from ATP in the proximal tubule and the renal collecting ducts, the latter being of special importance.
Increased inorganic phosphate intake increases urine PPi excretion. This may reflect inhibition of PPi hydrolysis. Because of the link, higher urine phosphate excretion and urine phosphate concentration may mirror higher urine PPi levels, accounting for our finding that urine phosphate concentration appears strongly correlated with the CaP ULM.
Where Should We Go From Here?
Howsoever much I am entranced by the myriads of urine protein crystal inhibitors urine PPi and citrate as controllers of the ULM for CaP is an easier mark. Surely experiments can be devised to test the idea directly that these two simple molecules acting together account for over half of the ULM elevation in urine and therefore for over half of the protective distance between SS and the Ostwald limit.
If I were doing active bench research, I would work on this issue. My research colleagues are in fact planning to do exactly that this very spring.
What about the ULM – SS Distance
In part, the higher ULM from citrate and PPi will raise this distance for any degree of urine supersaturation.
But there is a trick to it.
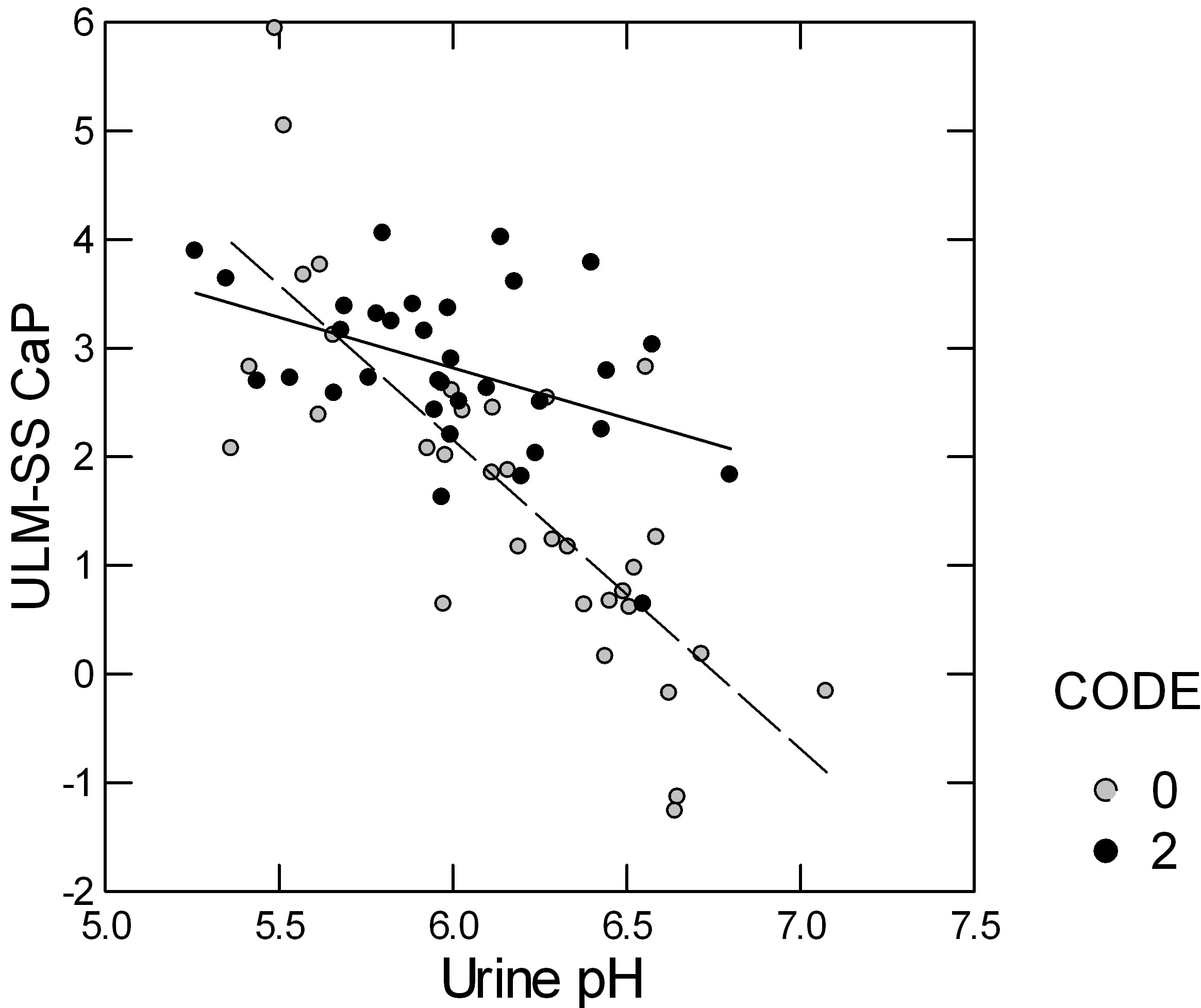 Urine CaP SS rises as urine pH rises but the CaP ULM is measured at a constant pH of 6.4 so if, for example, stone formers were to have a higher urine pH than normals their ULM – SS distance would fall simply because of the pH, all things considered.
Urine CaP SS rises as urine pH rises but the CaP ULM is measured at a constant pH of 6.4 so if, for example, stone formers were to have a higher urine pH than normals their ULM – SS distance would fall simply because of the pH, all things considered.
This led me to ask if the distance was indeed affected by urine pH, and indeed I found it was.
Here is a plot of the ULM – SS for CaP in patients (open circles) and normal people (closed circles). The distance falls in both but more steeply in the patients than in the normals. In part the steeper slope is because the patients include more high pH urine samples than the normals.
In a stepwise linear model, in which the ULM – SS distance is the dependent variable, only urine pH and whether the urines came from patients or normal controls entered; urine volume, calcium, citrate, phosphate, and gender, lost all significance. I believe this is correlation result is simply because of the unbalanced pH effect, being fixed in the ULM measurement and variable in the urine SS calculation.
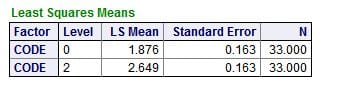
But, in the model, the mean values for the ULM – SS distance differed between the patients (0) and normals (2), even when we allowed for the urine pH: SS values at the ULM were 1.876 for patients and 2.849 for normals, which differed very significantly.
This remaining difference is perhaps due to something more than citrate because citrate did not enter the regression. Possibly it is the long sought effects of the great mass of urine protein inhibitors – perhaps not. LIke the question about PPi and citrate, the matter needs to resolved by new experiments.
Am I Happy I Brought This Topic to You?
I am.
Certainly we need more to explain stone formation than supersaturation, and that ‘more’ should be related to the inhibitory properties of urine. Of all the measurements our group made in these two studies, only the ULM – SS distance for CaP held up as a differentiating trait of patients from normal controls. So to understand the ULM is to understand something crucial about stone formers, something that remains to this day mysterious.
Everyone knows that supersaturation, howsoever basic to all crystallization, is not a sufficient explanation for why one person will form stones and another will not. It is our communal failure this past five decades that we have not as yet discovered the remaining explanations and provided proper measurements for clinical care.
Should citrate and inorganic pyrophosphate prove in experiments to be as important as our analysis suggests, the missing measurement – pyrophosphate – may well be a kind of breakthrough.
It is because there is mystery and importance I am happy I have brought this topic to your attention. Mystery and importance are what scientists come for, come to, are aroused by. This is the first time on this site I have introduced you to science in immediate evolution.
I hope you have enjoyed the ride.


I enjoyed the ride very much, Fred. I will have to take the ride again to really get it, I think, but it was helpful even the first time. You have done a nice job at taking decades of thinking and condensing it into a readable account.
Do you think that micro-environments can differ in the upper limit of metastability? That is, can the ULM be a ‘local’ phenomenon? Specifically, can crystallization adjacent to papillary cells have different ULM’s for CaP versus CaOx than further out in the calcyceal urine? We’ve talked about this some, but I am wondering what you think about the real possibilities. Thanks.
Thanks for the nice words, Jim, but even more for the perceptive question. How can it not be local, now that you bring the matter up. For example, if we are near cells which can produce and transport inorganic pyrophosphate (PPi) the ULM must be higher if PPi is really important in tubule fluid. As for the papillary epithelium – urothelium – I do not know if it can transport or produce PPi; it may. Likewise, proteins that are abundant or not in urine may be the opposite near cells that produce or possibly degrade them. We can assay ULM in very small samples. Would calyceal urine be an outstanding sample to assay? It sure would. Thanks!